Graphs in Go: implementation and some algorithms

Before I begin, let me note that I will be using two sources for algorithms in this article: Skiena - The Algorithm Design Manual (2nd edition), and Cormen, Leiserson, Rivest, and Stein - Introduction to Algorithms (3rd edition). I'll refer to these as ADM and CLRS, respectively.

In this article, I will implement a few graph algorithms in Go, in part to better learn the language, and in part to refresh my memory of working with graphs. Eventually, I would like to visualize these algorithms as well, and I will probably do that by "piping" them into graphviz.

For now, there are two types of tasks at hand: the first is populating the graph given some source data (from user input, a file, a database, etc), and the other is processing the graph once it's populated.

---

Implementation

---

Both of the above tasks depend on the question: how is the graph actually implemented in code? There are multiple options with various pros and cons, but I will leave that discussion to the books I've mentioned above (or whichever resource you find useful). Roughly following the approach of ADM and CLRS, our graph implementation will have the following properties:

• vertices are represented by integers
• the number of vertices is static (this is not really necessary but it makes representation of edges via a fixed-length slice work easily)
• edges are directed
• edges are stored using adjacency lists – that is, every vertex will have an associated slice of edges where said vertex is the source of each such edge

Finally, the source of data will be manually-entered vertex and edge data in the main() function, because this is the easiest way.

The graph will be represented in code as the struct type:

type Graph struct {
  nverts int
  edges  []*edge 
}

type edge struct {
  target int
  weight int
  next   *edge
}

Let's unpack this a little bit. First, since vertices are ints, there is no vertex type to keep track of. So, where "are" the vertices? Well, they are the ints 0 through nverts-1. And how do edges work? Each edge consists of a target, a weight, and a pointer to the next edge. The key thing to grok here is that the adjacency list for the vertex s is represented as edges[s]. In other words, edges[s] is a linked list of edges, where each such edge represents an edge of the form s --w--> t.

An initialization function for a graph might look like:

func New(n int) Graph {
  e := make([]*edge, n)
  g := Graph{nverts: n, edges: e}
  return g
}

so if we write g := New(10), this creates a graph with 10 vertices and no edges.

The last thing on the "graph creation" list is to write a function for adding edges. Say we want to add a new edge s --> t. The simplest way to do this is probably to add an edge as the head of edges[s]:

func (g *Graph) addEdge(s int, t int, w int) error {
  if s >= g.nverts || s < 0 || t >= g.nverts || t < 0 {
    return errors.New("invalid vertex")
  }
  e := edge{target: t, weight: w, next: g.edges[s]}
  g.edges[s] = &e
  return nil
}

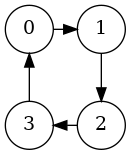we can add edges as follows:

func main() {
  g := New(4)
  g.addEdge(0, 1, 0)
  g.addEdge(1, 2, 0)
  g.addEdge(2, 3, 0)
  g.addEdge(3, 0, 0)
}

Oh, and we can print edges like so:

func printEdges(g Graph) {
  for src, head := range g.edges {
    // Iterate through edges with src as source
    for e := head; e != nil; e = e.next {
      fmt.Printf("%d --%d--> %d\n", src, e.weight, e.target)
    }
  }
}

0 --0--> 1
1 --0--> 2
2 --0--> 3
3 --0--> 0

---

Algorithms – BFS

---

Now that we have a model for storing a graph in memory, let's implement a breadth-first search (BFS). I will be basing the implementation off of a mix between ADM and CLRS, but there are differences. Before getting into the differences, let's briefly look at what the algorithm does.

In a lot of places (see for example: Wikipedia's article, or maybe your favorite Leetcode problem), BFS is used to find a specified node, and return true or false whether or not it finds that node. The algorithm described in ADM and CLRS is slightly different: it is used for exploration. The search will explore the entire graph – well, a connected component, as we will see later – starting at some source node, and the algorithm will not exit after finding some target node. Additionally, we will call a function process_vertex immediately after dequeueing a vertex v from the queue in our main loop, and a function process_edge for each edge with v as its source. This gives us the flexibility to use bfs to accomplish different tasks (we will see this later), based on what we put in these "processing" functions.

Let's discuss how our code will differ from ADM and CLRS.

First, we won't implement the tri-coloring scheme: white/grey/black or undiscovered/discovered/processed. The tri-color scheme is good for visualization purposes but not necessary for the actual BFS algorithm. Instead, we can simplify this and use an undiscovered/discovered scheme, which is pretty standard in many sources you may come across.

Second, we will write the bfs function so that it takes the above-mentioned process_vertex and process_edge functions as parameters. In ADM, these functions are accessible from bfs, but this presents issues for two reasons that I can see. One reason is that we would have to change the global process_vertex each time we want to implement a different algorithm (e.g. checking connected components or bipartite-ness). With the input parameter setup, we can define the processing functions locally inside each of our algorithm functions and pass them to the bfs function, so that bfs acts as a sort of template. The other reason is that this will be a great way (for me, at least) to feel more comfortable with functions-as-parameters and closures.

Okay, all of that said, here's what an adaptation of the above looks like:

func bfs(g Graph, start int, process_vertex func(v int), 
         process_edge func(s int, t int)) {
  if start < 0 || start >= g.nverts {
    return
  }
  if process_vertex == nil {
    process_vertex = func(v int) {}
  }
  if process_edge == nil {
    process_edge = func(s int, t int) {}
  }

  queue := make([]int, 0, g.nverts)
  disc := make([]bool, g.nverts)
  
  queue = append(queue, start)
  disc[start] = true

  for len(queue) != 0 {
    v := queue[0]
    process_vertex(v)
    queue = queue[1:]
    head := g.edges[v]
    // Process edges with v as source
    // Enqueue all neighbors
    for e := head; e != nil; e = e.next {
      process_edge(v, e.target)
      if !disc[e.target] {
        disc[e.target] = true
        queue = append(queue, e.target)
      }
    }
  }
}

Notice that there is a little bit of validation for the start vertex, and that if we pass nil for our processing functions, we will just make them empty. The rest of this is adapted straight from ADM. In particular, process_edge takes two ints, because we need to operate with the source and target (e.g. in bipartite checking) but the source isn't included in an edge type. Another possibly is to make it of the type func(src int, e edge).

To illustrate the modularity afforded to us by passing process_vertex as a parameter, let's print all of the vertices as we come across them in the BFS. In this case, the content of process_vertex should be something like

so our function to print the BFS looks like:

func bfsPrint(g Graph, start int) {
  process_vertex := func(v int) {
    fmt.Printf("%d\n", v)
  }
  bfs(g, start, process_vertex, nil)
}

If we then add

to our main(), then we get the output:

0
1
2
3

Let's play with this function a bit to make sure we understand what's going on. If we instead call bfsPrint(g,1) then we get:

1
2
3
0

If we add an edge with g.addEdge(0,2,0), our graph will look like:

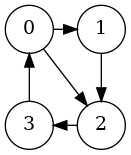
If we call bfsPrint(g,0) again, then we get:

0
2
1
3

Alright, one more example, which will lead us into the next section. What happens if we add three more vertices, and connect two of those with edges, so our main() is now:

func main() {
  g := New(7)
  g.addEdge(0, 1, 0)
  g.addEdge(1, 2, 0)
  g.addEdge(2, 3, 0)
  g.addEdge(3, 0, 0)
  g.addEdge(0, 2, 0)
  g.addEdge(4, 5, 10)
  g.addEdge(5, 4, 20)
  bfsPrint(g, 0)
}

0
2
1
3

---

Algorithms – counting connected components

---

To count connected components, the idea is to run BFS on each vertex. Well, sort of. We can do a bit better if we keep track of what we've discovered already, and avoid searching on those vertices a second time. In ADM, the "discovered" array is a global variable accessed from the bfs function, so the connected_components function can also access this array to check what's been discovered.

Because we're not using a global variable, we don't have access to the disc slice from outside of bfs, which makes things a little awkward. However, we can mimic the behavior in ADM by passing a new disc slice from our components function. This approach takes advantage of function closures: we can create a disc slice in the components function, and send that to bfs as the process_vertex function. This allows us to update our disc slice during logic inside bfs. Pretty cool!

We can put this together into a function which will return the number of connected components in our graph:

func components(g Graph) int {
  disc := make([]bool, g.nverts)
  count := 0

  process_vertex := func(v int) {
    fmt.Printf("found %d in component %d\n", v, count)
    disc[v] = true
  }

  for i := 0; i < g.nverts; i++ {
    // only start a new bfs on vertices we haven't seen yet
    if !disc[i] {
      count++
      bfs(g, i, process_vertex, nil)
    }
  }

  return count
}

Just to stress this again: note that there are two different disc slices at play, independent of each other – one in components and one in bfs.

If we run components(g) against our graph we built earlier, we get 3. Why three and not two? Well, if you recall, we made our graph size seven, so there's a vertex, 6, floating out there with no edges to or from it. Our graph looks like:

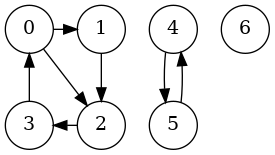
In fact, the full output of the above code also prints the vertices it finds in each component, so we can see the order in which the function is being called:

found 0 in component 1
found 2 in component 1
found 1 in component 1
found 3 in component 1
found 4 in component 2
found 5 in component 2
found 6 in component 3
3

---

Algorithms – checking if bipartite

---

Another algorithm that bfs can help with is an algorithm to check if a graph is bipartite. A graph is bipartite if the set of vertices can be divided into two disjoint sets, such that any edge in the graph runs between the two disjoint sets, and no edge exists between two vertices in the same set.

Again, we'll adapt the algorithm from ADM. The idea is to color vertices either white or black, as we discover them. We will run the bfs on each component in a range like in our components function. We will start out coloring the first vertex white, and then for each edge running from that vertex, we will try to color each of the target vertices black. In general the algorithm proceeds like this: we process every edge – using process_edge – and for each vertex, we try to color its neighbors the opposite color. If we come across an edge where both the source and target have already been colored, and those colors are the same, then our graph cannot be bipartite. It's worth thinking a bit about why this algorithm actually works. It turns out, it is equivalent to checking if the graph has an odd-length cycle.

The code for this looks like:

func bipartite(g Graph) bool {
  bipartite := true
  disc := make([]bool, g.nverts)
  colors := make([]uint8, g.nverts) // 0 nothing; 1 white; 2 black

  complement := func(v int) uint8 {
    if colors[v] == 1 {
      return 2
    }
    if colors[v] == 2 {
      return 1
    }
    return 0
  }

  // keep track of discovered to initialize colors in new components
  process_vertex := func(v int) {
    disc[v] = true
  }

  process_edge := func(s int, t int) {
    if colors[s] == colors[t] {
      bipartite = false
      fmt.Printf("Not bipartite due to conflict: %d --> %d\n", s, t)
    }
    colors[t] = complement(s)
  }

  for i := 0; i < g.nverts; i++ {
    if !bipartite {
      break
    }
    if !disc[i] {
      colors[i] = 1
      bfs(g, i, process_vertex, process_edge)
    }
  }

  return bipartite
}

One note to make: in our process_edge, we need to check the color of the source vertex. This is why, as mentioned earlier in the BFS section, we need the source and target as input parameters, rather than making the function a nicer-looking type like func(e edge).

As usual, let's run some example tests. We'll add fmt.Println(bipartite(g)) to main(), and our graph is still:

Running the program, we get:

$ go run graph.go
Not bipartite due to conflict: 1 --> 2
Not bipartite due to conflict: 3 --> 0
false

Let's unpack this to make sure we understand the algorithm. The algorithm starts on 0 and colors it white. There are two edges with source 0: 0 --> 2 and 0 --> 1. The former is the head of edges[0] and gets processed first, so 2 gets colored black and added to the queue. Then 0 --> 1 is processed and 1 gets colored black and added to the queue. Now 2 dequeued and the edge 2 --> 3 is processed, which means 3 is colored white and added to the queue. So far so good. But now we dequeue 1 and process 1 --> 2. The algorithm checks the colors of these vertices and notices that they are both colored black, so our graph cannot be bipartite (we discovered an odd cycle).

Our program also found a conflict with 3 --> 0, but it could have ended after finding the 1 --> 2 conflict. I'm not entirely sure how to approach this yet, to short-circuit bfs from the outside. See the end of the next section for more on this issue.

If we remove the edge 1 --> 2 and re-run the program, we get the output true. This version of the graph is bipartite because we can color 0 and 2 white, 1 and 3 black, so the component 1 is okay. For component 2 (i.e. the 4 <--> 5 part), we color 4 white and 5 black, and 6 white.

---

Algorithms – searching for a specified vertex

---

Finally, let's talk briefly about an algorithm that a lot of people might think of as being BFS – an algorithm which searches the graph for a specific vertex, and returns true or false depending whether or not the vertex is in our graph. We can also leverage our bfs to help us run this algorithm. Again we will use the function closure scheme, and keep track of a boolean in process_vertex.

This might look like:

// Return true if search is found; false otherwise
func bfsFind(g Graph, search int) bool {
  found := false

  process_vertex := func(v int) {
    if v == search {
      found = true
    }
  }

  for i := 0; i < g.nverts; i++ {
    if found {
      break
    }
    bfs(g, i, process_vertex, nil)
  }

  return found
}

There is a big efficiency problem with this approach though, which also existed with bipartite above. The short-circuiting when search is found happens in bfsFind, not in bfs. This means that, even if the vertex is found in bfs, the algorithm will finish searching the entire connected component that contains search before it returns to bfsFind.

I can't think of a good way to fix this issue at the moment, but I will ruminate about it. I'm not sure if there is a way to short-circuit bfs by using our process_vertex function, but I doubt it.

Optimization aside, the algorithm does work:

// fmt.Println(bfsFind(g, 0))
true
// fmt.Println(bfsFind(g, 5))
true
// fmt.Println(bfsFind(g, 8))
false
// fmt.Println(bfsFind(g, -1))
false

---

Next time

---

This is a good place to stop. Next time, I'd like to dive into more complicated algorithms that use edge weights, perhaps come up with a better solution to the bfsFind problem, and start to look at visualizing these algorithms.

Thanks for reading.